이진트리 중 이진탐색트리를 구별하는 방법을 설명하시오.
이진탐색트리 : 중위순회시 나오는 원소가 오름차순임.
이진트리 탐색하는 경우 시간 복잡도가 최선, 최악인 경우는?
최선 : 완전이진트리
최악 : 편향트리(한쪽 노드로만 연결되어있는 트리)
이진트리를 배열과 연결리스트로 구현하는 경우(장단점)
배열
장점 : 노드의 위치를 인덱스를 통해 접근 가능
단점 : 완전이진트리가 아닌 편향트리 같은 경우 기억공간 낭비가 심할 수 있다.
연결리스트
장점 : 기억장소 절약, 노드의 삽입/삭제 용이
단점 : 이진트리가 아닌 일반트리의 경우 각 노드의 차수만큼 가변적인 포인터를 할당해야 함.
Binary Heap이 되기 위한 조건 두가지는?
완전이진트리어야 함.
Max Heap or Min Heap을 만족해야 함.
힙이란 무엇인가?
완전이진트리를 기본으로 하는 자료구조이다. 최대값이나, 최소값을 검색하는 시간복잡도는 O(1)이다.
힙, 이진트리 사용 예
힙 : 우선순위 큐, 힙 정렬, 하프만 코드
이진트리 : 이진탐색트리
힙과 이진탐색트리의 공통점과 차이점은?
공통점 : 둘다 이진트리다.
차이점 : 힙은 각 노드의 값이 자식 노드보다 크다. 이진탐색트리의 경우 왼쪽자식이 가장 작고, 부모, 오른쪽자식 순으로 크다.
AVL 트리란?
왼쪽, 오른쪽 자식 트리 간의 깊이 차이가 1이하인 이진 탐색 트리.
일반적인 경우의 힙구성과 힙정렬, 힙 삽입시, Heapify, 이진탐색트리의 시간복잡도는?
힙구성, 힙 삽입, Heapify : O(logN)
힙 정렬 : O(NlogN)
이진탐색트리 : 평균O(logN), 최악O(N)
트리와 그래프의 차이점은?
순회와 비순회 (트리- 비순회 // 그래프 - 순회 가능)
Heapify 과정을 설명하시오.
자식노드와 비교하면서 우선순위에 따라 값을 변경한다(MaxHeap: 자식이 큰 값, MinHeap: 자식이 작은 값과 변경)
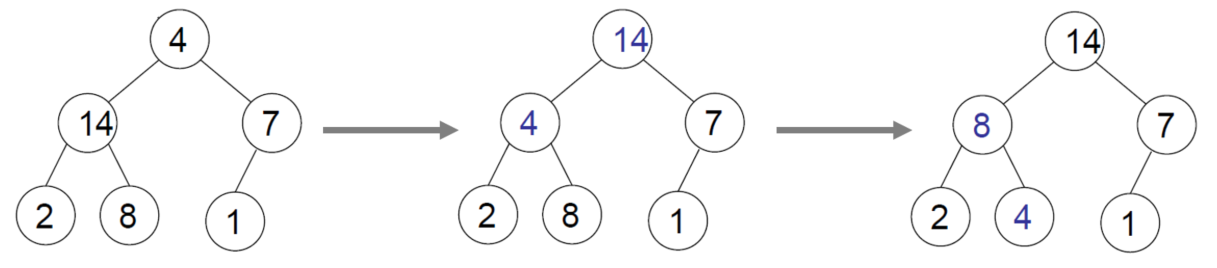
//재귀로 구현
private void maxHeapify(int pos) {
// 자식 노드가 부모노드보다 클 경우
if (Heap[pos] < Heap[leftChild(pos)] || Heap[pos] < Heap[rightChild(pos)]) {
// 자식 2개 비교 후 왼쪽 자식이 더 크면
if (Heap[leftChild(pos)] > Heap[rightChild(pos)]) {
//왼쪽 자식과 swap
swap(pos, leftChild(pos));
maxHeapify(leftChild(pos));
//반대는 오른쪽 자식과 swap
} else {
swap(pos, rightChild(pos));
maxHeapify(rightChild(pos));
}
}
}